« »

Рубрика: Комбинации геометрических тел

Вписанный в шар цилиндр

Рассмотрим комбинацию тел: шар и вписанный в шар цилиндр. 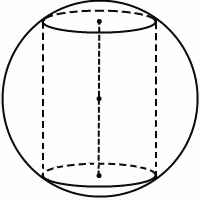цилиндр вписан в шар

Цилиндр вписан в шар, если окружности его оснований лежат на поверхности шара. В этом случае говорят также, что шар описан вокруг цилиндра. Центр шара лежит на середине оси цилиндра.

 

 

 

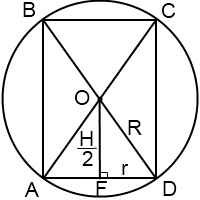осевое сечение цилиндра и шара Как и при решении задач на шар, вписанный в цилиндр, чаще всего рассматривают сечение комбинации тел плоскостью, проходящей через ось цилиндра. Это сечение представляет собой вписанный в окружность прямоугольник, стороны которого равны высоте конуса и диаметру его основания. Центр окружности лежит на пересечении диагоналей  прямоугольника.

Рассмотрим пример такого осевого сечения. Здесь точка O — центр описанного около цилиндра шара, BD — диаметр шара, OD=R — радиус шара, AB=H — образующая и высота цилиндра, AD — диаметр цилиндра, FD=r — радиус цилиндра.

    \[\angle ABD = \frac{1}{2}\angle AOD\]

(как вписанный и центральный углы, опирающиеся на одну дугу AD).

Треугольник AOD — равнобедренный (AO=OD=R), в нем OF=H/2 — высота, медиана и биссектриса.

Треугольник OFD — прямоугольный. По теореме Пифагора получаем соотношение, связывающее радиус шара с радиусом и высотой вписанного в шар цилиндра:

    \[O{D^2} = O{F^2} + F{D^2}, \Rightarrow \]

    \[{R^2} = {(\frac{H}{2})^2} + {r^2}.\]

Это же соотношение можно получить из прямоугольного треугольника ABD: по теореме Пифагора

    \[B{D^2} = A{D^2} + A{B^2}, \Rightarrow \]

    \[{(2R)^2} = {(2r)^2} + {H^2}\]

    \[{R^2} = {r^2} + \frac{{{H^2}}}{4}.\]

Ваш отзыв , 25 Фев 2013

Ваш отзыв