Рассмотрим примеры заданий из №7 ЕГЭ, в которых нужно найти точки экстремума на графике производной.
Точка xo, в которой существует производная f'(xo), является точкой экстремума функции f(x), если производная в этой точке равна нулю и при переходе через xo производная меняет свой знак.
Отсюда следует, что в точках экстремума функции график производной должен не просто касаться оси Ox, он должен её пересекать.
№1
На рисунке изображён график производной функции f(x), определённой на интервале (-6;7). Найти точку экстремума функции f(x) на отрезке [-2;5].
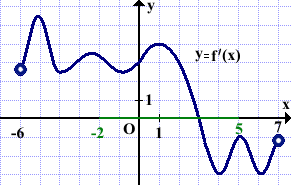
Решение:
На рисунке изображён график производной (а не график функции)!
В точках экстремума функции производная f'(x) равна нулю и меняет знак.
Выделяем отрезок [-2;5]. Точка, в которой производная равна нулю и меняет знак — это точка с абсциссой 3.
Значит x=3 — точка экстремума функции y=f(x).
Ответ: 3.
№2
На рисунке изображён график производной функции f(x), определённой на интервале (-9;5). Найти количество точек экстремума функции f(x) на отрезке [6-;4].
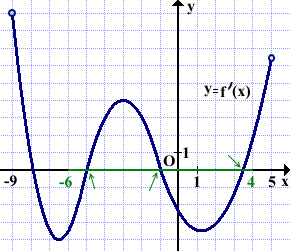
Решение:
Выделяем отрезок [-6;4].
На этом отрезке график производной пересекает ось абсцисс в трёх точках.
Следовательно, на отрезке [-6;4] функция f(x) имеет три точки экстремума.
Ответ: 3.
№3
На рисунке изображён график производной функции f(x), определённой на интервале (-7;7). Найти количество точек экстремума функции f(x) на отрезке [-5;6].
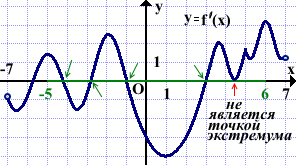
Решение:
Выделяем отрезок [-5;6].
На этом отрезке график производной пересекает ось абсцисс в четырёх точках. Значит, функция f(x) имеет на отрезке [-5;6] четыре точки экстремума.
Точка, в которой производная равна нулю, но знак не меняет (график производной коснулся оси Ox, но не пересёк её), не является точкой экстремума.
Ответ: 4.
Важно внимательно читать условие, чтобы не перепутать нахождение точек экстремума по графику производной с заданием на нахождение точек экстремума по графику функции!