Рассмотрим решение тригонометрических неравенств вида tgx>a и tgx<a на единичной окружности.
Для решения нам потребуется чертеж единичной окружности и линия тангенсов. Радиус единичной окружности равен 1, поэтому, откладывая на линии тангенсов отрезки, длина которых равна радиусу, получаем соответственно точки, в которых тангенс равен 1, 2, 3 и т.д., а вниз — -1,-2,-3 и т.д.
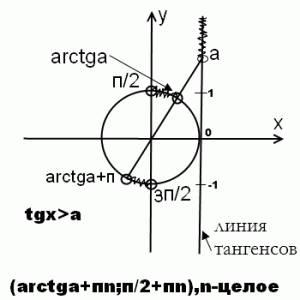
1) tgx>a
На линии тангенсов значениям тангенсов, большим a, соответствует часть, расположенная выше точки а. Заштриховываем соответствующий луч. Теперь проводим прямую через точку О — начало отсчета- и точку а на линии тангенсов. Она пересекает окружность в точке arctg a. Соответственно, на окружности решению неравенства tgx>a соответствует дуга от точки arctg a до п/2. Чтобы учесть все решения (а их с учетом периодичности тангенса — бесконечное множество), к каждому концу интервала прибавляем пn, где n — целое число (n принадлежит Z).
Для решения неравенства tgx>a вполне достаточно полуокружности от -п/2 до п/2. Но если требуется найти, к примеру, решение системы неравенств с тангенсом и синусом, то нужна вся окружность.
Если неравенство нестрогое, точку с arctg a включаем в ответ (на рисунке ее заштриховываем, в ответ записываем с квадратной скобкой). Точка п/2 в ответ никогда не включается, поскольку не входит в область определения тангенса (точка выколотая, скобка круглая).
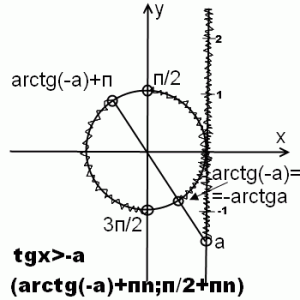
2) tgx>-a
Чтобы решить неравенство tgx>-a, рассуждаем так же как и для неравенства tgx>a. Поскольку arctg (-a)=-arctg a, только этим и отличается ответ.
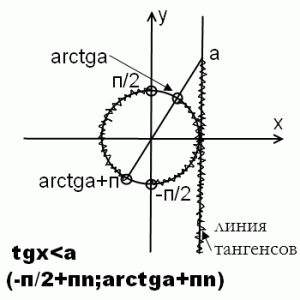
3) tgx<a
В этом случае решению неравенства tgx<a соответствует часть линии тангенсов, расположенная ниже a. Соответственно, поскольку промежуток мы всегда записываем от меньшего к большему, в этом случае решение начинается от -п/2 и идет к arctg a.
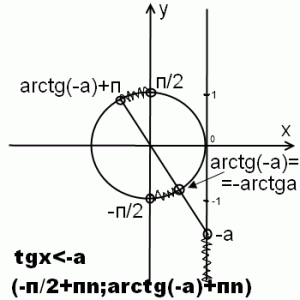
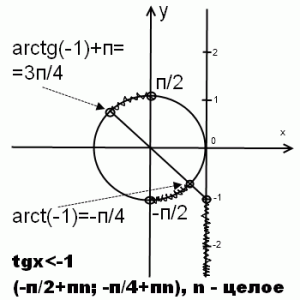
4) tgx<-a
Решение неравенства tgx<-a аналогично решению неравенства tgx<a с той разницей, что arcg (-a)=-arctg a.
Рассмотрим конкретный пример решения неравенства с тангенсом.
Решить неравенство tgx<-1
Таким образом, решение неравенства tgx<-1 есть открытый промежуток (-п/2+пn; -п/4+пn).
Здравствуйте.
Такое впечатление, что решение неравенств с тангесами писал совершенно другой человек. Фактически НИКАКИХ объяснений. Ни слова не сказано о том, как находить второй угол. Очень жаль.
Никаких объяснений?