Продолжим рассмотрение экзаменационных тестовых заданий.
Тесты с таблицей показывают, как связаны между собой переменные (в первой таблице задается сумма переменных, во второй — произведение).
Внизу таблицы записано, что требуется определить на основании данных задачи.
Универсальный способ решения — алгебраический: составить систему уравнений, решить её, полученные результаты использовать для нахождения значения выражения.
Можно попробовать определить значение выражения и другими способами, не решая системы уравнений.

Показать решение
D).
Из первой таблицы b+b=c, c+c=a+b, то есть 2b=c, 2c=a+b. Из второй — b∙b=a, то есть b²=a.
Имеем систему уравнений:
![Rendered by QuickLaTeX.com \[\left\{ \begin{array}{l} 2b = c\\ 2c = a + b\\ {b^2} = a \end{array} \right.\]](https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-63751ed915e12ae6516842217aee479c_l3.png)
Подставим c=2b и a=b² во 2-е уравнение:
2∙2b=b²+b, b²-3b=0, b1=3, b2=0.
Если b=3, c=2∙3=6, a=a=3²=9, a∙c=6∙9=54.
b=0 не подходит.
(Другой способ.
Если умножить 1-е и 2-е уравнение, 2b³=a∙c. Следовательно, половина произведения a∙c является кубом некоторого числа. Из предложенных вариантов ответов только 54 удовлетворяет этому условию (половина 54 — 27 — куб 3).
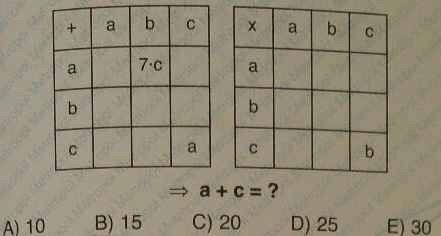
Показать решение
B).
Из первой таблицы следует, что a+b=7∙c и c+c=a, из второй — c∙c=b. То есть, 2c=a и c²=b. Следовательно, a+b=2c+c²=7∙c.
2c+c²=7∙c
c²-5∙c=0
с=0 или c=5.
Отсюда a=0 или a=10.
При c=5, a=10 a+c=15.
(c=0, a=0 не подходят).

Показать решение
B).
Из первой таблицы следует, что b+b=c, то есть 2b=c, из второй — a∙a=b (то есть a²=b), a∙b=3∙c.
Умножив обе части равенства 2b=c на 3, получим 6b=3c. Так как a∙b=3∙c,
то a∙b=6b, откуда a=6 (при b≠0).
b=a²=6²=36.
A+B=6+36=42.

Показать решение
D).
Из первой таблицы b+c=a, из второй — a∙b=K, b∙b=a+4, a∙c=L, c∙c=a-1. Имеем систему уравнений:
![Rendered by QuickLaTeX.com \[\left\{ \begin{array}{l} b + c = a\\ ab = K\\ {b^2} = a + 4\\ ac = L\\ {c^2} = a - 1 \end{array} \right.\]](https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-ab7a083713db019e5eca3bd5e8287544_l3.png)
Нам не нужно решать ее, нам требуется лишь найти K-L. Вычтем почленно из 2-го уравнения 4-е: ab-ac=K-L, a(b-c)=K-L.
Вычтем почленно из 3-го уравнения 5-е:
b²-c²=(a+4)-(a-1),
(b-c)(b+c)=a+4-a+1=5.
Так как b+c=a, a(b-c)=5.
Следовательно, K-L=5.

Показать решение
C).
Из первой таблицы a+c=b/2, b+c=8∙a, из второй — a∙a=b, то есть, a²=b.
Из 1-го уравнения почленно вычтем 2-е:
a-b=b/2-8a, отсюда 9a=3b/2, b=6a. Подставляем b=6a в 3-е уравнение: a²=6a. Отсюда a=6 (a=0 не подходит), b=6a=6∙6=36.
Так как a+c=b/2, 6+c=36/2, с=12.

Показать решение
D).
Из первой таблицы a+c=5b, b+b=c, (то есть 2b=c), из второй — b∙b=a+4 (b²=a+4). Имеем систему уравнений:
![Rendered by QuickLaTeX.com \[\left\{ \begin{array}{l} a + c = 5b\\ 2b = c\\ {b^2} = a + 4 \end{array} \right.\]](https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-d34735ce9425ba016466b6fd9df57293_l3.png)
Подставим c=2b во 2-е уравнение: a+2b=5b, откуда a=3b.
Подставим a=3b в 2-е уравнение: b²=3b+4, b²-3b-4=0, b1=4, b2=-1.
Если b=4, c=2∙4=8, a=3∙4=12.
b=-1 не подходит.
a+b+c=12+4+8=24.
И еще пару заданий без таблиц.

Показать решение
D).
Число внутри «звезды» равно сумме произведений чисел, стоящих в «лучах» напротив друг друга.
I: 3∙2+2∙1+3∙2=14,
II: 4∙1+3∙2+4∙3=22,
III: 3∙1+2∙5+4∙2=21.

Показать решение
A). Число вверху круга на 7 больше разности чисел, стоящих внизу:
I: 99-76=23, 23+7=30,
II: 66-53=13, 13+7=20,
III: 105-87=18, 18+7=25.
В следующий раз рассмотрим тестовые задания, в которых нужно найти периметр фигуры по рисунку.

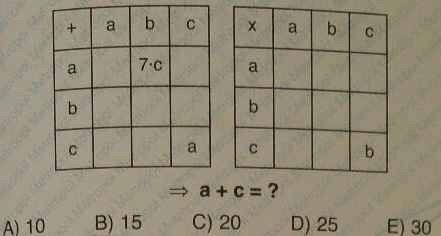






![Rendered by QuickLaTeX.com \[\left\{ \begin{array}{l} 2b = c\\ 2c = a + b\\ {b^2} = a \end{array} \right.\]](https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-63751ed915e12ae6516842217aee479c_l3.png)
![Rendered by QuickLaTeX.com \[\left\{ \begin{array}{l} b + c = a\\ ab = K\\ {b^2} = a + 4\\ ac = L\\ {c^2} = a - 1 \end{array} \right.\]](https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-ab7a083713db019e5eca3bd5e8287544_l3.png)
![Rendered by QuickLaTeX.com \[\left\{ \begin{array}{l} a + c = 5b\\ 2b = c\\ {b^2} = a + 4 \end{array} \right.\]](https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-d34735ce9425ba016466b6fd9df57293_l3.png)