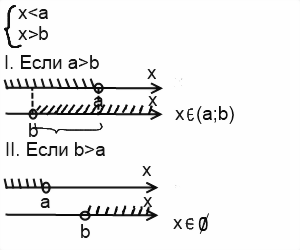
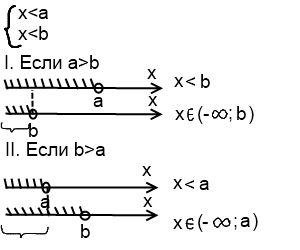« »

Рубрика: Легкое решение

Системы линейных неравенств с одной переменной

Системы линейных неравенств с одной переменной сводятся к одному из видов

Решение систем линейных неравенств

 

 

 

 

 

 

 

 

 

 

система двух линейных неравенств

 

 

 

 

 

 

 

 

 

 

линейные неравенства в системе

 

 

 

 

 

 

 

 

 

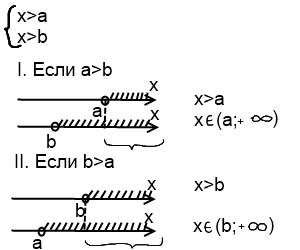
Пользуясь этим  коротким правилом, решение систем линейных неравенств можно упростить. Правило очень легко запомнить:

Больше большего

Меньше меньшего

Если система состоит из неравенств одного знака, то не нужно рисовать координатные прямые и искать решение как пересечение решений   неравенств, а можно сразу записать ответ.

Например,

    \[1)\left\{ \begin{array}{l}x > 5\\x > 18\end{array} \right. \Rightarrow x > 18\]

Оба знака — «больше», поэтому применяем правило»больше большего». Большее из 5 и 18 — 18, поэтому и пришли к выводу x>18.

    \[2)\left\{ \begin{array}{l}x < - 7\\x < 12\end{array} \right. \Rightarrow x < - 7\]

Здесь оба знака — «меньше», по правилу «меньше меньшего» решением выбираем меньшее их данных чисел, и получаем x<-7.

Особенно облегчает это правило решение системы линейных неравенств, состоящей из большого количества неравенств. Например,

    \[3)\left\{ \begin{array}{l}x > 3\\x > - 7\\x > 14\\x > 9\end{array} \right. \Rightarrow x > 14\]

Пользуясь этим правилом, систему линейных неравенств, состоящую из нескольких неравенств с разными знаками, можно свести к системе всего из двух неравенств:

    \[4)\left\{ \begin{array}{l}x > 5\\x < 8\\x > - 3\\x > 2\\x < - 7\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x > 5\\x < - 7.\end{array} \right.\]

 

 

Ваш отзыв , 06 Мар 2013

Ваш отзыв