Рассмотрим решение тригонометрических неравенств вида синус меньше a (sinx<a) на единичной окружности.
Синус — это ордината точки. Соответственно, sinx=a в точках пересечения единичной окружности и прямой y=a. Часть окружности, расположенная выше прямой y=a, соответствует значениям синуса, большим a. Поскольку мы решаем неравенство sinx<a, его решениям будет соответствовать часть окружности, расположенная ниже прямой y=a. Рассмотрим несколько вариантов взаимного расположения прямой y=a и единичной окружности.
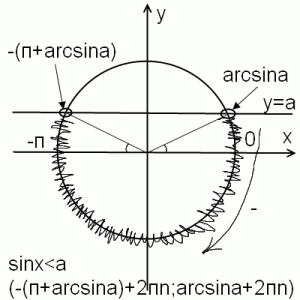
1) sinx<a при 0<a<1
Основная задача здесь — правильно определить точки пересечения прямой и окружности. Первая точка находится легко — это arcsina. Для определения второй точки рассуждаем так: так как sin<a, нам нужна часть окружности под прямой y=a. Значит, из первой точки во вторую идем нижним путем, то есть по часовой стрелке. Но при движении по часовой стрелке угол уменьшается. От arcsina мы дошли до 0, а дальше пошли отрицательные углы (точнее, сам угол положительный, а минус — всего лишь знак обхода от нуля по часовой стрелке). Таким образом мы доходим до -п, и переходим за него ровно на arcsina. Поскольку мы прошли п и еще arcsina, мы к п прибавляем arcsina. А так как движение шло по часовой стрелке, то перед суммой ставим знак минус.
Мы нашли только один интервал, на котором sinx<a. Чтобы учесть все решения (а таких интервалов — бесконечное множество), с учетом периодичности синуса к каждому из концов интервала прибавляем 2пn, где n — целое число (то есть n принадлежит Z).
Если неравенство нестрогое, точки пересечения окружности и прямой закрашиваем, а затем включаем в решение (круглую скобку заменяем на квадратную).
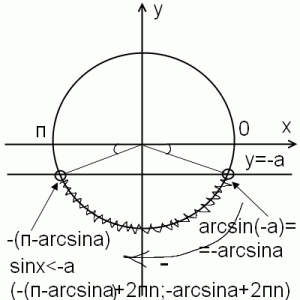
2) sinx<-a при 0<a<1
Первая точка arcsin(-a)=-arcsina. Чтобы попасть во вторую, идем нижним путем, то есть по часовой стрелке. До п, точнее до -п, не доходим на arcsina. Поэтому вторая точка — (п-arcsina). Мы не дошли до угла п arcsina, а поскольку движение происходит по часовой стрелке, то перед разностью ставим знак минус. Чтобы учесть все решения, к обоим концам промежутка прибавляем 2пn, где n — целое число.
Для нестрого неравенства точки закрашиваем и включаем в ответ (с квадратной скобкой вместо круглой).
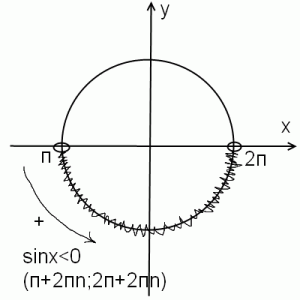
3) sinx<0
В этом случае удобнее решение записывать не от нуля до -п, а от п до 2п. Для нестрогого неравенства- квадратные скобки, закрашенные точки.
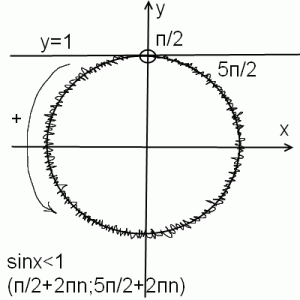
4) sinx<1
И в этом случае тоже удобнее выбирать положительные точки. Решением данного неравенства являются все x, кроме п/2+2пn. Чтобы записать это в виде промежутка, надо определить его концы. Если первую точку взять п/2, то во вторую мы попадем через полный оборот окружности, то есть п/2+2п=5п/2. К обоим концам прибавляем 2пn.
![]()
В этом случае никакие точки не исключаются, а значит, x — любое число:(-∞;+∞).
![]()
В этом случае единственной точкой на окружности, удовлетворяющей данному условию, является точка -п/2. С учетом периодичности синуса решение данного неравенства — множество точек вида x=-п/2+2пn, где n — целое число.
7) sinx<a при a>1
Окружность в этом случае целиком лежит ниже прямой y=a, а значит, решением данного неравенства является любое значение x: (-∞;+∞).
8) sinx< -a при a>1
Окружность целиком лежит выше прямой y=a, а значит, нет ни одного x, удовлетворяющего условию неравенства. Значит, решений нет.
И в заключении, рассмотрим пример.
Решить неравенство sinx<-1/2
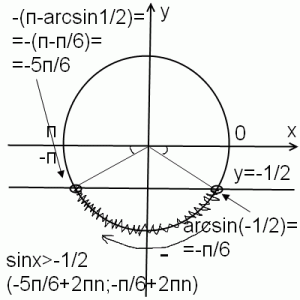
супер — очень доходчиво — спасибо