Шар, вписанный в цилиндр, касается оснований цилиндра в их центрах, а боковой поверхности цилиндра — по параллельной основаниям окружности большого круга (то есть радиус этой окружности равен радиусу шара).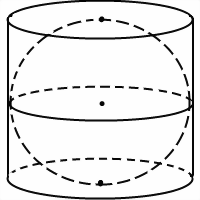
Если шар вписан в цилиндр, то цилиндр описан около шара.
В цилиндр можно вписать шар тогда и только тогда, когда цилиндр равносторонний, то есть его высота равна диаметру. Радиус вписанного в цилиндр шара R равен радиусу цилиндра r:
R=r.
Решение задач на шар, вписанный в цилиндр, чаще всего сводится к рассмотрению осевого сечения комбинации тел.
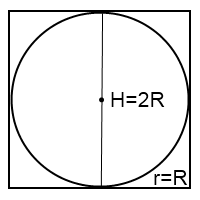
Это сечение представляет собой квадрат с вписанной в него окружностью. Сторона квадрата равна высоте цилиндра и диаметру шара:
H=2R
Найдем отношение объема цилиндра к объему вписанного в него шара. Объем шара
![\[{V_1} = \frac{4}{3}\pi {R^3}\]](https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-3aeac8fe1322cb51ef3583b070433b25_l3.png "Rendered by QuickLaTeX.com")
Объем цилиндра
![\[{V_2} = \pi {r^2}H = \pi {R^2} \cdot 2R = 2\pi {R^3}.\]](https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-7823fe8f5a2d83d5dbdd3c8d2dc3c060_l3.png "Rendered by QuickLaTeX.com")
Отсюда отношение объема шара к объему описанного около него цилиндра
![\[\frac{{{V_1}}}{{{V_2}}} = \frac{{\frac{4}{3}\pi {R^3}}}{{2\pi {R^3}}} = \frac{2}{3}.\]](https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-aeb582ff44d51131c4f084a5ff84fb7f_l3.png "Rendered by QuickLaTeX.com")
Теперь найдем отношение площади поверхности цилиндра к площади вписанного шара. Площадь поверхности шара (площадь сферы)
![\[{S_1} = 4\pi {R^2}\]](https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-0af25186c13d42fc17a54d9db507577b_l3.png "Rendered by QuickLaTeX.com")
Площадь полной поверхности цилиндра равна сумме площадей оснований и боковой поверхности:
![\[{S_2} = {S_{bok}} + 2{S_{ocn}} = 2\pi rH + 2\pi {r^2} = \]](https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-14e351b9dfdc39bdf2163c9adae12a81_l3.png "Rendered by QuickLaTeX.com")
![\[ = 2\pi R \cdot 2R + 2\pi {R^2} = 6\pi {R^2}.\]](https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-d2f24908d3d109190dff0f96c1e8cdbf_l3.png "Rendered by QuickLaTeX.com")
Отсюда отношение площади поверхности вписанного шара к площади поверхности цилиндра
![\[\frac{{{S_1}}}{{{S_2}}} = \frac{{4\pi {R^2}}}{{6\pi {R^2}}} = \frac{2}{3}.\]](https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-dd44c7ae65e5c1b8f18ffa927a00aaf7_l3.png "Rendered by QuickLaTeX.com")
В цилиндр вписан шар. Расстояние между точками касания шара с боковой поверхностью и основанием цилиндра равно 2 корня из 2 см. Найдите площадь полной поверхности цилиндра
Треугольник, вершины которого — центр шара и точки касания шара с боковой поверхностью и основанием цилиндра — прямоугольный равнобедренный. Катеты равны радиусу шара и цилиндра и половине высоты цилиндра, гипотенуза известна. Следовательно, R=H/2=2, H=4. Площадь полной поверхности цилиндра равна S=2πR(R+H)=2π∙2∙(2+4)=24π см².