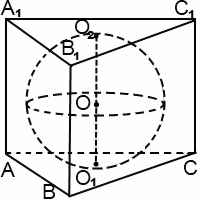
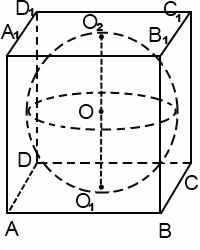
Шар, вписанный в призму

« Вписанный в шар цилиндр Трапеция вписана в окружность »

Шар, вписанный в призму

Шар вписанный в призму, касается каждой ее грани. Диаметр вписанного шара равен высоте призмы, а также равен диаметру окружности, вписанной в основание призмы.

шар, вписанный в призму

Центр шара лежит на середине высоты призмы, проведенной через центр вписанной в основание окружности. Если в основание призмы нельзя вписать окружность либо высота призмы не равна диаметру вписанной в основание окружности, то в такую призму шар вписать нельзя.

Если призма правильная, центр вписанного в нее шара является точкой пересечения бисекторных плоскостей призмы.

При решении задач на шар,вписанный в призму, можно рассмотреть сечение комбинации тел плоскостью, параллельной основаниям. Она представляет собой многоугольник, равный многоугольнику основания, с вписанной в него окружностью, радиус которой равен радиусу шара. Далее используем формулы, связывающие радиус вписанной окружности со сторонами основания, а также то, что центр вписанной в многоугольник окружности является точкой пересечения его биссектрис.

Выразим объем призмы через радиус вписанного шара — R. Объем призмы равен

${V_n} = {S_{ocn}} \cdot H$

Площадь основания ищем по формуле S=pr, где p — полупериметр основания, r — радиус вписанной в него окружности. Поскольку в нашем случае r=R и высота призмы H=2R, то

${V_n} = pR \cdot 2R = 2p \cdot {R^2}$

Но 2p=P — периметру основания. Окончательно имеем

${V_n} = P{R^2}$

Выразим площадь полной поверхности прямой призмы через радиус вписанного в нее шара. Площадь полной поверхности прямой призмы равна сумме площадей оснований и боковой поверхности:

${S_{n.n.}} = {S_{bok}} + 2{S_{ocn}}$