Решение неравенств методом интервалов

« Метод интервалов. Примеры Рисунок ромба »

Решение неравенств методом интервалов

Рассмотрим решение неравенств методов интервалов для случаев, когда один и тот же корень в примере встречается несколько раз.

$1)\frac{{{x^2} - 8x + 12}}{{2x - {x^2}}} \le 0.$

Используем алгоритм метода интервалов. Приравниваем к нулю левую часть:

$\frac{{{x^2} - 8x + 12}}{{2x - {x^2}}} = 0 \Leftrightarrow \left\{ {\begin{array}{*{20}{l}} {{x^2} - 8x + 12 = 0,}\\ {2x - {x^2} \ne 0.} \end{array}} \right.$

Отсюда

$\left\{ \begin{array}{l} x = 6,x = 2,\\ x \ne 0,x \ne 2. \end{array} \right.$

Корень х=2 встречается 2 раза, то есть четное число раз. Значит, в точке х=2 — «петля». Точки х=2 и х=0 — выколотые, поскольку в них знаменатель обращается в нуль. Так как неравенство нестрогое, точка х=6 — закрашенная.

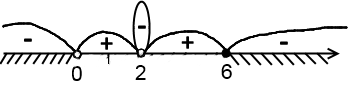
Metodintervalov

Для проверки знака берем 1. Подставляя ее в последнее неравенство, получаем отрицательное число. Значит на интервале (0;2), которому принадлежит 1, ставим «+». Остальные знаки расставляем в шахматном порядке. Поскольку левая часть меньше либо равна нулю, в ответ записываем промежутки с «-«.

Ответ: х∈(-∞;0)U[6;∞).

$2)\frac{{({x^2} - 6x - 27)({x^2} - 9x)}}{{25 - {x^2}}} \ge 0.$

Приравниваем к нулю левую часть:

$\frac{{({x^2} - 6x - 27)({x^2} - 9x)}}{{25 - {x^2}}} = 0 \Leftrightarrow$

$\left\{ \begin{array}{l} ({x^2} - 6x - 27)({x^2} - 9x) = 0;\\ 25 - {x^2} \ne 0; \end{array} \right.$

$\left\{ \begin{array}{l} x = 9,x = - 3,x = 0,x = 9;\\ x \ne - 5,x \ne 5 \end{array} \right.$

Полученные точки отмечаем на числовой прямой. Поскольку неравенство нестрогое, точки закрашенные (кроме точек, в которых знаменатель обращается в нуль). Так как корень х=9 встречается четное число раз (2 раза), в нем — «петля».

как решать неравество методом интервалов. Пример

Для проверки знака берем 1. Подставив ее в последнее неравенство, получаем положительное число. Остальные знаки расставляем в шахматном порядке. Нам нужны промежутки с «+». Не забываем включить в ответ отдельно стоящую закрашенную точку.

Ответ:

$x \in \left( { - 5; - 3} \right] \cup \left[ {0;5} \right) \cup \left\{ 9 \right\}.$

$3)\frac{{({x^2} - 8x + 16)(x + 10)}}{{{x^2} - 16}} \le 0.$

Приравниваем к нулю левую часть:

$\frac{{({x^2} - 8x + 16)(x + 10)}}{{{x^2} - 16}} = 0 \Leftrightarrow$

$\left\{ \begin{array}{l} ({x^2} - 8x + 16)(x + 10) = 0;\\ {x^2} - 16 \ne 0; \end{array} \right.$

$\left\{ \begin{array}{l} x = 4,x = - 10;\\ x \ne - 4,x \ne 4. \end{array} \right.$

Если квадратное уравнение х²-8х+16=0 решать через дискриминант, получаем D=0, а значит, корень х=4 — кратный корень второй степени. Но есть еще одно уравнение с корнем х=4. Таким образом, корень х=4 встречается три раза, то есть нечетное количество. Значит, «петли» в нем нет. (Если решать уравнение по теореме Виета, получаем х1=х2=4 и еще один корень х=4. Итого, 3 раза).

пример решения неравенства методом интервалов