Решение методом интервалов

« Как решать неравенства методом интервалов Метод интервалов. Примеры »

Решение методом интервалов

Теперь рассмотрим решение методом интервалов более сложных неравенств. Начнем с неравенств, содержащих кратные корни четных степеней.

$1){(x - 1)^2}{(x + 2)^3}{(x - 5)^4}{(x - 10)^5} > 0.$

Используем алгоритм решения неравенств методом интервалов. Приравниваем к нулю левую часть:

${(x - 1)^2}{(x + 2)^3}{(x - 5)^4}{(x - 10)^5} = 0$

${(x - 1)^2} = 0;{(x + 2)^3} = 0;{(x - 5)^4} = 0;{(x - 10)^5} = 0$

$x = 1;x = - 2;x = 5;x = 10.$

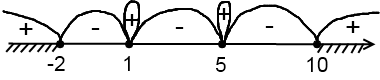
Полученные точки отмечаем на числовой прямой. Неравенство строгое, все точки — выколотые. Корни х=1 и х=5 — кратные корни четной степени, поэтому в них — «петля»:

решение неравенств методом интервалов, кратные корни

Для проверки знака берем нуль и подставляем его в последнее неравенство. Получаем (+)∙(+)∙(+)∙(-), итого (-). Остальные знаки расставляем в шахматном порядке. Нам нужен знак «+», соответственно, выбираем промежутки с «+».

Ответ:

$x \in \left( { - \infty ; - 2} \right) \cup \left( {10;\infty } \right).$

Рассмотрим еще три варианта решения этого же примера с разными знаками неравенства.

$2){(x - 1)^2}{(x + 2)^3}{(x - 5)^4}{(x - 10)^5} \ge 0.$

В отличие от предыдущего примера, данное неравенство нестрогое, поэтому точки в этом случае — закрашенные:

как решать неравенства методом интервалов

Отдельно стоящие закрашенные точки включаем в решение!

Ответ:

$x \in \left( { - \infty ; - 2} \right] \cup \left\{ {1;5} \right\} \cup \left[ {10;\infty } \right).$

$3){(x - 1)^2}{(x + 2)^3}{(x - 5)^4}{(x - 10)^5} < 0.$

Неравенство строгое, точки — выколотые. В этом неравенстве нам нужен знак «-«:

метод интервалов для решения неравенств

Ответ:

$x \in \left( { - 2;1} \right) \cup \left( {1;5} \right) \cup \left( {5;10} \right).$

$4){(x - 1)^2}{(x + 2)^3}{(x - 5)^4}{(x - 10)^5} \le 0.$

От предыдущего неравенства это отличается только тем, что является нестрогим. Соответственно, точки в нем — закрашенные, и они входят в решение:

решить неравенство методом интервалов

Ответ:

$x \in \left[ { - 2;10} \right].$

$5)\frac{{(x + 3){{(x - 2)}^6}}}{{{{(x + 1)}^7}}} \le 0.$

Приравниваем к нулю левую часть:

$\frac{{(x + 3){{(x - 2)}^6}}}{{{{(x + 1)}^7}}} = 0 \Leftrightarrow \left\{ \begin{array}{l}(x + 3){(x - 2)^6} = 0,\\{(x + 1)^7} \ne 0,\end{array} \right.$

$\Leftrightarrow \left\{ \begin{array}{l}x = - 3;x = 2,\\x \ne - 1.\end{array} \right.$

Полученные точки отмечаем на числовой прямой. Неравенство нестрогое, точки — закрашенные. Только точка, в которой знаменатель обращается в нуль, выколотая (всегда!).

решение методом интервалов, неравенства с кратными корнями