Рассмотрим задания, в которых требуется найти промежутки убывания функции по графику производной.
№1
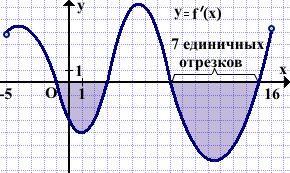
На рисунке изображён график функции y=f'(x) — производной функции f(x), определённой на интервале (-5;16). Найти промежутки убывания функции f(x). В ответ указать длину наибольшего из них.
 Решение:
Решение:
На промежутках убывания функции y=f(x) её производная y=f'(x) отрицательна.
Выделяем промежутки, на которых производная y=f'(x) принимает отрицательные значения. В данном случае таких промежутком два: (-1;3) и (8;15). Так как в точках -1, 3, 8 и 15 существует производная f'(x), то функция f(x) непрерывна в этих точках. Поэтому эти точки можно включать в промежутки возрастания и убывания. Таким образом, функция y=f(x) убывает на промежутках [-1;3] и [8;15].
Длины этих промежутков равны четырём и семи единичным отрезкам.
Ответ: 7.
№2
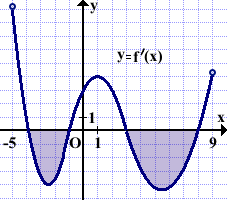
На рисунке изображён график функции y=f'(x) — производной функции f(x), определённой на интервале (-5;9). Найти промежутки убывания функции f(x). В ответе указать сумму целых точек, входящих в эти промежутки.
 Решение:
Решение:
На промежутках убывания функции y=f(x) её производная y=f'(x) отрицательна.
Выделяем промежутки, на которых производная y=f'(x) принимает отрицательные значения. В данном примере таких промежутков два: (-4;-1) и (3;8).
Так как в точках -4, -1, 3 и 8 существует производная f'(x), то функция f(x) непрерывна в этих точках. Поэтому эти точки можно включить в промежутки убывания. Следовательно, функция y=f(x) убывает на промежутках [-4;-1] и [3;8].
Найдём сумму целых точек, входящих в эти промежутки:
-4+(-3)+(-2)+(-1)+3+4+5+6+7+8=23.
Ответ: 23.
№3
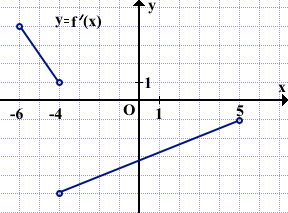
Функция f(x) определена и непрерывна на интервале (-6;5). На рисунке изображен график её производной. Найти промежутки убывания функции f(x). В ответе указать сумму целых точек, входящих в эти промежутки.
 Решение:
Решение:
На промежутках убывания функции y=f(x) её производная f'(x) отрицательна. В данном примере производная f'(x)<0 на интервале (-4;5).
По условию, функция f(x) непрерывна на интервале (-6;5). Поэтому точку -4, входящую в этот интервал, можно включить в промежуток убывания. Таким образом, функция f(x) убывает на полуинтервале [-4;5).
Найдём сумму целых точек, входящих в промежуток [-4;5):
(-4)+(-3)+(-2)+(-1)+0+1+2+3+4=0.
Ответ: 0.