Рассмотрим задания, в которых дан график производной функции и требуется найти, в какой точке данного отрезка эта функция принимает наибольшее значение.
№1
На рисунке изображён график производной функции f(x), определённой на интервале (-14;8). В какой точке отрезка [-11;-8] функция f(x) принимает наибольшее значение?
Решение:
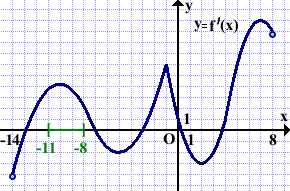 Выделяем отрезок [-11;-8].
Выделяем отрезок [-11;-8].
На этом отрезке производная f'(x) принимает положительные значения.
Следовательно, функция f(x) на этом отрезке возрастает, то есть бо́льшему значению аргумента соответствует бо́льшее значение функции:
x1,x2 ∈[-11;-8], x2>x1, ⇒ f(x2)>f(x1).
Поэтому наибольшее значение функция f(x) на отрезке принимает при наибольшем значении аргумента, то есть на правом конце отрезка, при x=-8.
Ответ: -8.
№2
На рисунке изображён график производной функции f(x), определённой на интервале (-7;9). В какой точке отрезка [4;8] функция f(x) принимает наибольшее значение?
Решение:
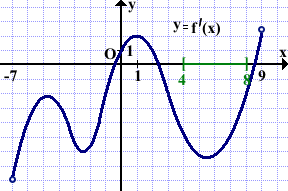 Выделяем отрезок [4;8].
Выделяем отрезок [4;8].
Так как этом отрезке производная f'(x)<o, то функция f(x) на [4;8] убывает, то есть бо́льшему значению аргумента соответствует меньшее значение функции:
x1,x2 ∈[4;8], x2>x1, ⇒ f(x2)<f(x1).
Поэтому наибольшее значение f(x) принимает в этом случае при наименьшем значении аргумента, то есть на левом конце отрезка, при x=4.
Ответ: 4.
№3
Функция y=f(x) определена на промежутке (-5;9). На рисунке изображён график её производной. Найти абсциссу точки, в которой функция y=f(x) принимает наибольшее значение.
Решение:
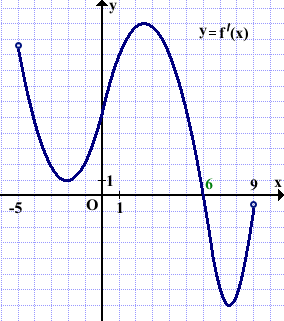 В точке с абсциссой x=6 производная меняет знак с плюса на минус.
В точке с абсциссой x=6 производная меняет знак с плюса на минус.
Следовательно, x=6 — точка максимума.
Производная f'(x) существует на всём интервале (-5;9), следовательно, функция f(x) непрерывна на (-5;9).
Если непрерывная функция f(x) имеет на заданном интервале (a;b) только одну точку экстремума xo и это точка максимума, то на (a;b) функция принимает своё наибольшее значение в точке xo.
Таким образом, функция f(x) на интервале (-5;9) принимает наибольшее значение в точке x=6.
Ответ: 6.
№4
Функция y=f(x) определена и непрерывна на отрезке [-1;9]. На рисунке изображён график её производной. Найти точку xo, в которой функция принимает наибольшее значение, если f(-1)≥f(9).
Решение:
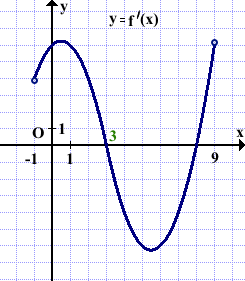 На промежутках (-1;3) и (8;9) производная f'(x)>0, поэтому на этих промежутках функция f(x) возрастает.
На промежутках (-1;3) и (8;9) производная f'(x)>0, поэтому на этих промежутках функция f(x) возрастает.
На промежутке (3;9) производная f'(x)<0, поэтому на (3;9) функция f(x) убывает.
Так как функция определена и непрерывна на отрезке [-1;9], то точки -1, 3, 8 и 9 можно включать в промежутки монотонности.
Следовательно, на отрезках [-1;3] и [8;9] функция f(x) возрастает, на отрезке [3;8] — убывает.
На промежутках возрастания наибольшее значение функция принимает на правом конце отрезка. На [-1;3] наибольшее значение f(x) принимает в точке x=3 (точке максимума), на [8;9] — в точке x=9.
Так как на [-1;3] f(x) возрастает, то f(3)>f(-1). По условию, f(-1)≥f(9), значит f(3)>f(9).
Таким образом, наибольшее значение функции f(x) принимает в точке x=3.
Ответ: 3.