В стрессовых условиях экзамена или контрольной работы иногда забываются даже самые простые формулы. Этот способ помогает легко найти площадь боковой поверхности цилиндра, а также его полную поверхность.
Чтобы вывести нужные формулы, потребуется тетрадный лист. Соедините два его края так, чтобы получилась труба:
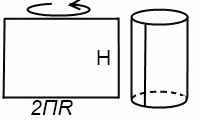
Поверхность трубы — боковая поверхность цилиндра. Теперь разворачиваем лист. Площадь боковой поверхности цилиндра равна площади развертки, то есть площади прямоугольника.
Формулу площади прямоугольника забыть сложно: S=ab — произведение его сторон.
В нашем случае одна сторона равна высоте цилиндра, вторая — длине окружности основания.
Перемножив H и 2ПR, получаем искомую формулу боковой поверхности цилиндра:
![\[{S_{b.n.}} = 2\pi RH.\]](https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-4f2250ea98f2ae06e41c4bd71a9fa830_l3.png "Rendered by QuickLaTeX.com")
Полная поверхность цилиндра состоит из боковой поверхности и двух оснований — кругов.
Отсюда площадь полной поверхности цилиндра
![\[{S_{n.n.}} = 2\pi RH + 2\pi {R^2}\]](https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-bb85a1d81d82af997593e087b68fc2db_l3.png "Rendered by QuickLaTeX.com")
или
![\[{S_{n.n.}} = 2\pi R(H + R).\]](https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-ca8caa4663ee81cbe6bfbc66ca275229_l3.png "Rendered by QuickLaTeX.com")
С площадью боковой поверхности цилиндра теперь ясно. А объём цилиндра как определить?
А про объемы — следующий пост. Там и про объем цилиндра есть.
Привет спасибо за хороший контент продолжайте в таком же духе желаю вам удачи ивсего доброго
Спасибо, Орман! И Вам успехов!