Узнать ещё

Рассмотрим свойства пирамид, в которых все боковые ребра равны, с  соответствующими чертежами.

Если все боковые ребра пирамиды равны между собой, то вершина пирамиды проецируется в центр описанной около основания окружности.

Прямоугольные треугольники, образованные высотой пирамиды, боковыми ребрами и их проекциями (равными радиусу описанной окружности), равны. Поэтому также

— все боковые ребра пирамиды образуют с плоскостью основания равные углы;

— все углы, которые боковые ребра образуют с высотой пирамиды,  равны.

Решение задач на пирамиду, в которой все боковые ребра равны (либо все боковые ребра образуют равные углы с основанием пирамиды или с высотой пирамиды) начинается с чертежа.

Если основание пирамиды — треугольник.

 

 

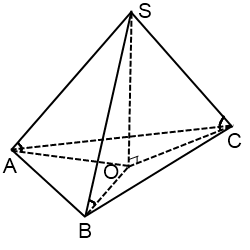
Центр окружности, описанной около остроугольного треугольника, лежит внутри треугольника.

OA=OB=OC=R

 

 

 

 

 

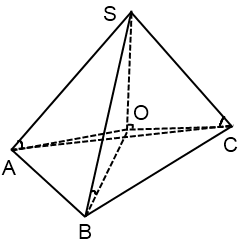
Центр окружности, описанной около тупоугольного треугольника, лежит вне треугольника.

OA=OB=OC=R.

На рисунке тупой угол — это угол B.

 

 

 

 

Радиус окружности, описанной около произвольного остроугольного либо тупоугольного треугольника ABC, можно найти по следствию из теоремы синусов:

   

либо по формуле

   

 

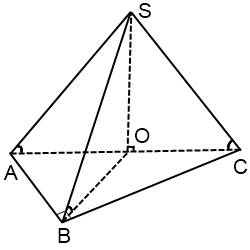
Центр описанной около прямоугольного треугольника окружности лежит на середине гипотенузы.

Радиус описанной около основания окружности в этом случае равен

   

где c — гипотенуза.

Отсюда для данного треугольника ABC с прямым углом B

   

 

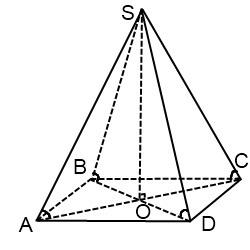
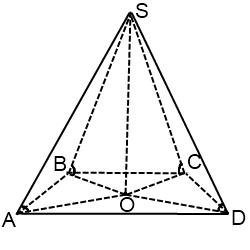
Если основание пирамиды — параллелограмм

Из всех параллелограммов описать окружность можем только около прямоугольника (квадрат — его частный случай). Поэтому, если в задаче сказано, что пирамиде все боковые ребра равны, либо все боковые ребра одинаково наклонены к плоскости основания, либо все боковые ребра образуют с высотой пирамиды равные углы, а в основании — параллелограмм, то это может быть только прямоугольник (квадрат).

Центр описанной около прямоугольника окружности — точка пересечения его диагоналей. Соответственно, радиус R равен половине диагонали прямоугольника.

 

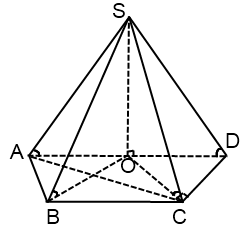
Если основание пирамиды -трапеция

Из всех трапеций описать окружность можно только около равнобочной трапеции.

Радиус описанной окружности ищем как радиус окружности, описанной около одного из треугольников ABC или ACD по одной из формул, приведенных выше.

 

 

 

 

 

Если диагональ трапеции перпендикулярна боковой стороне

 

В этом случае центр описанной около трапеции окружности лежит на середине большего основания, а высота пирамиды лежит в боковой грани, содержащей это большее основание.

Радиус R в этом случае — половина гипотенузы прямоугольного треугольника ACD.

 

 

 

 

 

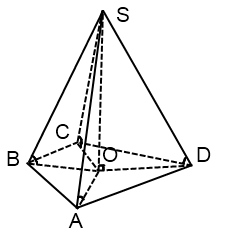
Если основание пирамиды — произвольный четырехугольник

Радиус описанной около основания окружности находим как радиус окружности, описанной около одного из треугольников основания: ABC, BCD, ACD или ABD.

Поскольку описать около четырехугольника окружность можно только тогда, когда сумма его противолежащих углов равна 180 градусов, то