« »

Рубрика: Виды пирамид

Пирамиды, в которых двугранные углы при основании равны

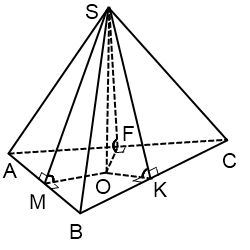
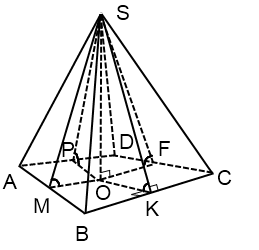
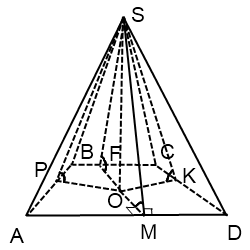
Теперь рассмотрим пирамиды, в которых двугранные углы при основании равны: каковы их свойства, как изображаются.

Если все двугранные углы при ребрах основания равны, то

1) вершина пирамиды проецируется в центр вписанной в основание окружности;

2) основание пирамиды является ортогональной проекцией ее боковой поверхности, поэтому площадь основания пирамиды можно найти по формуле

    \[{S_{ocn}} = {S_{bok}} \cdot \cos \varphi \]

где

    \[\varphi \]

— двугранный угол при основании пирамиды. Чаще эту формулу используют для нахождения площади боковой поверхности пирамиды:

    \[{S_{bok}} = \frac{{{S_{ocn}}}}{{\cos \varphi }}\]

Соответственно, площадь полной поверхности пирамиды равна

    \[{S_{n.n.}} = {S_{ocn}} + {S_{bok}} = {S_{ocn}}(1 + \frac{1}{{\cos \varphi }})\]

3) площадь боковой поверхности в этом случае также может быть найдена по формуле

    \[{S_{bok}} = pl\]

где p — полупериметр основания, l — высота боковой грани, проведенная из вершины пирамиды.

Прямоугольные треугольники, образованные высотой пирамиды, высотами боковых граней, проведенными из вершины пирамиды, и их проекциями (равными радиусу вписанной окружности), равны. Поэтому также

— высоты боковых граней, проведенные из вершины пирамиды, равны;

— высоты боковых граней образуют с высотой пирамиды равные углы.

Решение задач на пирамиды, в которых двугранные углы при основании равны (или — пирамиды, в которых высоты боковых граней равны либо образуют с высотой пирамиды равные углы), начинается с чертежа.

Если основание пирамиды — треугольник

Центр вписанной в треугольник окружности лежит строго внутри треугольника и является точкой пересечения его биссектрис.

высоты боковых граней пирамиды равны

 

OM=OK=OF=r

Радиус вписанной окружности ищем по формуле

    \[r = \frac{S}{p}\]

где S — площадь треугольника, p — его полу периметр.

 

 

 

Если в основании такой пирамиды лежит прямоугольный треугольник, чертеж немного иной.

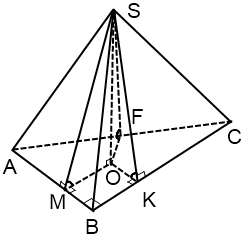боковые грани составляют с основанием пирамиды равные углыЭто связано со свойствами параллельного проектирования: параллельность прямых сохраняется. Радиусы, перпендикулярные катетам, и отрезки, прилежащие к прямому углу треугольника, образуют квадрат, который на чертеже изображается параллелограммом.

Радиус вписанной в прямоугольный треугольник окружности ищем по формуле

    \[r = \frac{{a + b - c}}{2}\]

где a и b — катеты, c — гипотенуза.

Если основание пирамиды — параллелограмм

основание пирамиды - параллелограмм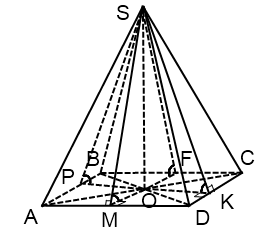Из всех параллелограммов вписать окружность можно только в ромб (и квадрат как его частный случай). Поэтому, если в задаче известно, что все двугранные углы при основании равны (или высоты боковых граней пирамиды равны либо образуют с высотой пирамиды равные углы), а в основании лежит параллелограмм, то речь может идти только о ромбе (или квадрате).

OM=OK=OF=OP.

O — точка пересечения диагоналей ромба (квадрата).

Радиус вписанной в ромб окружности можно искать по формуле

    \[r = \frac{S}{p}\]

Кроме того, радиус вписанной в ромб окружности равен половине его высоты.

Если  основание пирамиды — произвольный четырехугольник

двугранные углы при основании пирамиды равны

OM=OK=OF=OP=r

О — точка пересечения биссектрис четырехугольника ABCD.

Радиус вписанной в четырехугольник окружности ищем все по той же формуле

    \[r = \frac{S}{p}\]

Поскольку вписать в четырехугольник окружность можно тогда и только тогда, когда суммы длин его противоположных сторон равны,

AB+CD=BC+AD.

Если основание пирамиды — трапеция

в основании пирамиды лежит трапеция

OM=OK=OF=OP=r

O — точка пересечения биссектрис трапеции.

Радиус вписанной в трапецию окружности

    \[r = \frac{S}{p}\]

а также радиус вписанной окружности равен половине высоты трапеции.

Также AB+CD=BC+AD.

 

Если все двугранные углы при основании пирамиды равны (либо высоты боковых граней пирамиды равны, либо высоты боковых граней составляют с пирамидой равные углы), а в основании пирамиды — правильный многоугольник, то это — правильная пирамида.

 

Ваш отзыв , 12 Дек 2012

Ваш отзыв