Если в условии задачи сказано, что основание трапеции равно ее боковой стороне, то отсюда следует, что диагональ трапеции является биссектрисой ее угла.
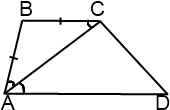 1) Если меньшее основание трапеции равно ее боковой стороне, то диагональ трапеции является биссектрисой прилежащего к этой боковой стороне острого угла.
1) Если меньшее основание трапеции равно ее боковой стороне, то диагональ трапеции является биссектрисой прилежащего к этой боковой стороне острого угла.
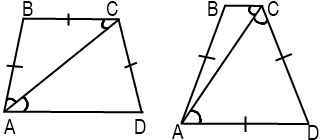
Рассмотрим трапецию ABCD, в которой боковая сторона AB равна меньшему основанию BC.
1) Так как AB=BC, треугольник ABC — равнобедренный с основанием AC. Значит, у него углы при основании равны:∠BAC=∠BCA.
2)∠BCA=∠∠CAD (как внутренние накрест лежащие при AD ∥ BC и секущей AC).
3) Отсюда следует, что ∠BAC=∠CAD, а значит, AC — биссектриса угла BAD.
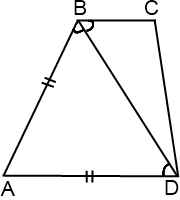 2) Если большее основание трапеции равно ее боковой стороне, то диагональ трапеции является биссектрисой прилежащего к этой боковой стороне тупого угла.
2) Если большее основание трапеции равно ее боковой стороне, то диагональ трапеции является биссектрисой прилежащего к этой боковой стороне тупого угла.
Рассмотрим трапецию ABCD, в которой большее основание AD равно ее боковой стороне AB.
1) Так как треугольник ABD — равнобедренный с основанием BD, то его углы при основании равны: ∠ABD=∠ADB.
2) ∠CBD=∠ADB (как внутренние накрест лежащие при AD ∥ BC и секущей BD).
3) Отсюда ∠CBD=∠ABD, следовательно, BD — биссектриса угла ABC.
Аналогично доказываются утверждения для прямоугольной и равнобедренной трапеции.
3) Если большее основание прямоугольной трапеции равно ее меньшей боковой стороне, диагональ является биссектрисой прямого угла, прилежащего к меньшему основанию.
4) Если меньшее основание прямоугольной трапеции равно ее меньшей боковой стороне, диагональ является биссектрисой прямого угла, прилежащего к большему основанию.
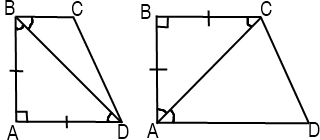
5) Если меньшее основание прямоугольной трапеции равно ее большей боковой стороне, диагональ является биссектрисой прилежащего к этой боковой стороне острого угла.
6) Если большее основание прямоугольной трапеции равно ее большей боковой стороне, диагональ является биссектрисой прилежащего к этой боковой стороне тупого угла.
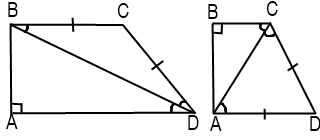
7) Если меньшее основание равнобедренной трапеции равно ее боковой стороне, то диагональ является биссектрисой острого угла трапеции.
8) Если большее основание равнобедренной трапеции равно ее боковой стороне, то диагональ является биссектрисой тупого угла трапеции.
В частности, так как сумма противолежащих углов равнобедренной трапеции равна 180º, соответственно, ∠ACD+3∠BCA=180º и ∠BAC+3∠CAD=180º.
спасибо!)
Огромное спасибо, очень помогло вспомнить то, что проводилось больше 30 лет назад, смогла решить и объяснить дочке задачу!
Наталья, Вас хорошо учили, раз вспомнили спустя столько лет. Успехов Вам и Вашей дочери!