Если в задача дана окружность, вписанная в равнобедренный треугольник, в ее решении могут быть использованы свойства касательных и свойство биссектрисы треугольника.
Замечание.
Центр вписанной в треугольник окружности является точкой пересечения его биссектрис. Поскольку в равнобедренном треугольнике биссектриса, проведенная к основанию, совпадает с медианой и высотой, то центр вписанной в равнобедренный треугольник окружности лежит на высоте и медиане, проведенных к основанию.
Рассмотрим две задачи на вписанную в равнобедренный треугольник окружность.
Задача 1.
Боковая сторона равнобедренного треугольника делится точкой касания вписанной окружности в отношении 8:9, считая от вершины угла при основании треугольника. Найти площадь треугольника, если радиус вписанной окружности равен 16 см.

Дано: ∆ ABC, AC=BC,
окружность (O, r) — вписанная,
F, K, M, — точки касания со сторонами AB, BC, AC,
AM:MC=8:9, r=16 см.
Найти:
![]()
Решение:
1) Пусть k — коэффициент пропорциональности (k>0). Тогда AM=8k см, MC=9k см.
2) По свойству касательных, проведенных из одной точки,
AF=AM=8k см, CK=MC=9k см.
Так как AC=BC, то BK=AM и BF=BK=8k см.
3) Центр вписанной окружности является точкой пересечения биссектрис треугольника.

Так как ∆ ABC — равнобедренный с основанием AB, то CF — высота, медиана и биссектриса ∆ ABC.
4) Рассмотрим треугольник AFC.
∠AFC=90, AF=8k см, AC=AM+MC=17k см.
По свойству биссектрисы треугольника:
![]()
OF=r. Пусть CO=x см, тогда
![]()
![]()
![]()
CO=34 см, CF=CO+OF=34+16=50 см.
По теореме Пифагора:
![]()
![]()
![]()
![]()
![]()
Таким образом,
![]()
![]()
![]()
Ответ: 1333 1/3 кв.см.
Задача 2.
Центр окружности, вписанной в равнобедренный треугольник, делит высоту, проведенную к основанию, в отношении 5:4. Найти периметр треугольника, если боковая сторона меньше основания на 15 см.
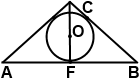 Дано: ∆ ABC, AC=BC,
Дано: ∆ ABC, AC=BC,
окружность (O, r) — вписанная,
CF — высота, CO:OF=5:4, AC<AB на 15 см.
Найти:
![]()
Решение:
 1) Рассмотрим ∆ ACF — прямоугольный (так как CF — высота треугольника по условию).
1) Рассмотрим ∆ ACF — прямоугольный (так как CF — высота треугольника по условию).
Центр вписанной в треугольник окружности есть точка пересечения его биссектрис.
По свойству биссектрисы треугольника,
![]()
или
![]()
Пусть k — коэффициент пропорциональности, тогда AC=5k см, AF=4k см, AB=2AF=8k см.
По условию, AC<AB на 15 см. Поэтому 8k-5k=15, 3k=15, k=5.
Следовательно, AC=BC=5∙5=25 см, AB=8∙5=40 см.
![]()
Ответ: 90 см.