Найти значение производной в точке

Рассмотрим задания, в которых по графику данной функции и касательной к нему в точке x_о требуется найти значение другой функции в точке x_о.

№1

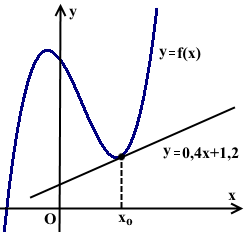
На рисунке изображён график функции y=f(x) и касательная к этому графику, проведённая в точке x_о. Уравнение касательной показано на рисунке. Найти значение производной функции g(x)=5f(x)-10x+9 в точке x_о.

najti-znachenie-proizvodnoj-v-tochke-po-grafiku Решение:

$g^/ (x) = (5f(x) - 10x + 9)^/ =$

$= 5f^/ (x) - 10;$

$g^/ (x_o ) = 5f^/ (x_o ) - 10.$

Осталось найти значение производной f'(x_о).
Угловой коэффициент касательной к графику функции y=f(x), проведённой в точке с абсциссой x_о, равен значению производной в точке касания: k=f'(x_о).

По условию, k=0,4. Поэтому f'(x_о)=0,4.

$g^/ (x_o ) = 5 \cdot 0,4 - 10 = - 8.$

Ответ: -8.

№2

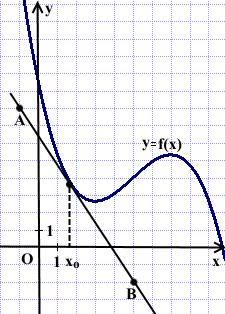
На рисунке изображён график функции y=f(x) и касательная к этому графику, проведённая в точке x_о. Найти значение производной функции g(x)=3f(x)+7x-5 в точке x_о.

Решение:

najti-znachenie-proizvodnoj-po-grafiku

$g^/ (x) = (3f(x) + 7x - 5)^/ =$

$= 3f^/ (x) + 7;$

$g^/ (x_o ) = 3f^/ (x_o ) + 7.$

Нужно найти значение производной f'(x_о).

f'(x_о)=k.

На графике касательной ищем две выделенные точки с целыми координатами: A(-1;8), B(5;-2).

Уравнение прямой имеет вид y=kx+b.

Так как эта прямая проходит через точки A и B, то их координаты удовлетворяют уравнению прямой.

Подставляем координаты A и B в уравнение прямой и из полученной системы уравнений находим k (для этого достаточно одно из уравнений системы умножить на -1 и сложить с другим уравнением).

$\left\{ \begin{array}{l} 8 = k \cdot ( - 1) + b; \\ - 2 = k \cdot 5 + b\_\_\_\left| { \cdot ( - 1);} \right. \\ \end{array} \right.$

$+ \frac{{\left\{ \begin{array}{l} 8 = - k + b; \\ 2 = - 5k - b; \\ \end{array} \right.}}{{10 = - 6k}}$

$k = - \frac{{10}}{6} = - \frac{5}{3}, \Rightarrow f^/ (x_o ) = - \frac{5}{3}.$

$g^/ (x_o ) = 3 \cdot \left( { - \frac{5}{3}} \right) + 7 = 2.$

Ответ: 2.

№3

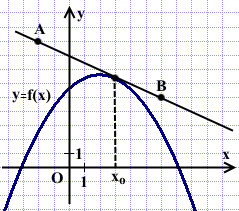
На рисунке изображён график функции y=f(x) и касательная к этому графику, проведённая в точке x_о=3. Найти значение производной функции g(x)=3x³-2f(x)+11 в точке x_о.

Решение:

najti-znachenie-proizvodnoj-v-tochke