Конус вписан в цилиндр

Конус вписан в цилиндр, если основание конуса совпадает с одним из оснований цилиндра, а вершина лежит в центре другого основания.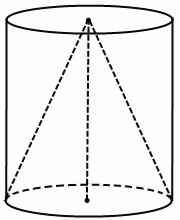

Оси цилиндра и вписанного в него конуса совпадают. Цилиндр и вписанный конус имеют равные высоты и радиусы.

Соответственно, в этом случае цилиндр описан около конуса.

Рассмотрим осевое сечение комбинации тел. Оно представляет собой прямоугольник с вписанным в него равнобедренным треугольником.

цилиндр описан около конуса сечение конуса, вписанного в цилиндр

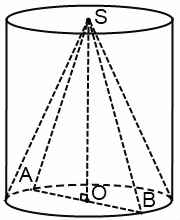
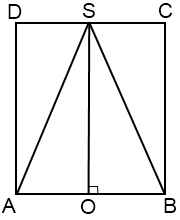
Здесь SO=H — высота цилиндра и вписанного конуса, OA=OB=R — радиус цилиндра и радиус конуса, SB=SA= l — образующая конуса, AD — образующая цилиндра.

Найдем отношение объема конуса к объему описанного около него цилиндра:

$\frac{{{V_1}}}{{{V_2}}} = \frac{{\frac{1}{3}\pi {R^2}H}}{{\pi {R^2}H}} = \frac{1}{3}.$

Из прямоугольного треугольника SOA по теореме Пифагора

$A{S^2} = A{O^2} + S{O^2}, \Rightarrow l = \sqrt {{R^2} + {H^2}} .$

Теперь найдем отношение площади боковой поверхности конуса к площади боковой поверхности описанного цилиндра:

$\frac{{{S_1}}}{{{S_2}}} = \frac{{\pi Rl}}{{2\pi RH}} = \frac{l}{{2H}} = \frac{{\sqrt {{R^2} + {H^2}} }}{{2H}}.$

Узнать ещё