« »

Рубрика: Задачи по планиметрии

Как перпендикуляр делит диаметр

Если в задаче дан перпендикуляр, опущенный из точки окружности на ее диаметр, чтобы выяснить, как перпендикуляр делит диаметр, и найти связь между полученными отрезками и длиной перпендикуляра, необходимо выполнить дополнительное построение.

перпендикуляр делит диаметр

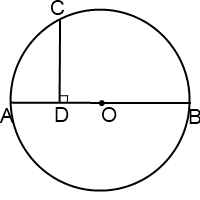
Пусть AB — диаметр окружности, С — точка окружности, а CD — перпендикуляр, проведенный из точки С к диаметру.

 

 

 

 

 

перпендикуляр, проведенный к диаметру

 

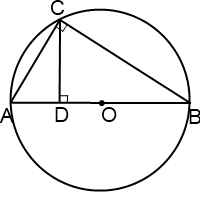
Соединим точку С с концами диаметра. Угол ACB — прямой (как опирающийся на диаметр). Следовательно, треугольник ABC  — прямоугольный, а CD в нем — высота, проведенная к гипотенузе.

Отсюда следует, перпендикуляр CD и отрезки AD и BD, на которые он делит диаметр — пропорциональные отрезки в прямоугольном треугольнике. А значит, они связаны соотношением:

    \[CD = \sqrt {AD \cdot BD} \]

Кроме того, в треугольнике ABC

    \[AC = \sqrt {AD \cdot AB} \]

    \[BC = \sqrt {BD \cdot AB} \]

Задача.

Перпендикуляр, опущенный из точки окружности на ее диаметр, делит диаметр на отрезки, разность которых равна 21 см. Найти радиус окружности, если длина перпендикуляра 10 см.

Решение:

перпендикуляр делит диаметр на отрезки

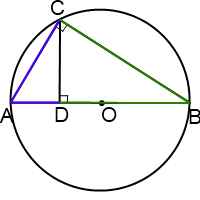
Проведем отрезки AC и BC.

∠ACB=90º(как вписанный угол, опирающийся на диаметр). Тогда в прямоугольном треугольнике ABC СD — высота, проведенная к гипотенузе. Поэтому

    \[CD = \sqrt {AD \cdot BD} \]

Пусть AD=x см, тогда BD=x+21см. Составляем уравнение:

    \[10 = \sqrt {x \cdot (x + 21)} \]

Возведем в квадрат обе части:

    \[x(x + 21) = 100\]

    \[{x^2} + 21x - 100 = 0\]

    \[{x_1} = 4,{x_2} = - 25\]

Второй корень — посторонний, так как длина отрезка не может быть отрицательным числом. Значит, диаметр AB=AD+BD=4+4+21=29см, а радиус равен половине диаметра, то есть r=14,5см.

Ответ: 14,5см.

 

Ваш отзыв , 29 Май 2013

Ваш отзыв