Узнать ещё

Задания, в которых на рисунке изображен график производной функции y=f ‘(x), и нужно определить точки экстремума и промежутки монотонности функции y=f(x), решаются очень просто. 

Достаточно помнить, что

1) функция y=f(x) возрастает на промежутках, где производная y=f ‘(x)>0;

2) функция y=f(x) убывает на промежутках, где производная y=f ‘(x)<0;

3) функция y=f(x) имеет критические точки, где производная f ‘(x)=0 или не существует (но это верно только для внутренних точек области определения, то есть точки на концах области определения не рассматриваем);

4) функция y=f(x) имеет точки экстремума там, где производная y =f ‘(x) меняет свой знак.

В частности, функция y=f(x) имеет точки максимума там, где производная меняет знак с плюса на минус;

функция y=f(x) имеет точки минимума там, где производная меняет знак с с минуса на плюс.

Примеры.

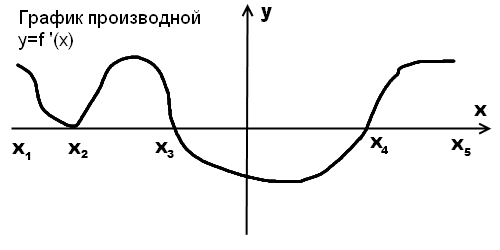
На рисунке изображен график производной функции. С помощью графика найти промежутки монотонности функции, критические точки, критические точки и точки экстремума.

 

 

 

 

 

 

 

Функция y=f(x) возрастает на промежутках (x1;x3) и (x4;x5) (то есть там, где производная y=f ‘(x) положительна, а значит, ее график расположен выше оси оx). Точку x2  не исключаем из промежутка возрастания — производная в этой точке равна нулю, но знак не меняет.

Функция y=f(x) убывает на промежутке (x3;x4) (то есть там, где производная y=f ‘(x) отрицательна, а значит, ее график расположен ниже оси оx).

Критические точки: x2, x3, x4. В этих точках производная обращается в нуль (а график производной, соответственно, пересекает ось ox).

x=x3 — точка максимума функции y=f(x), поскольку производная y=f ‘(x) в этой точке меняет знак с плюса на минус (график производной пересекает ox в направлении сверху вниз).

x=x4 — точка минимума функции y=f(x), так как производная y=f ‘(x) в этой точке меняет знак с минуса на плюс (график производной пересекает ox в направлении снизу вверх).

Точки экстремума: x3 и x4. В них производная не только обращается в нуль, но и меняет свой знак. Точка x=x2 — критическая, но точкой экстремума не является поскольку нет смены знака производной. То есть точки экстремума на графике производной — это те точки в которых график не касается, а пересекает ось ox.

 

 

 

 

 

 

 

 

 

 

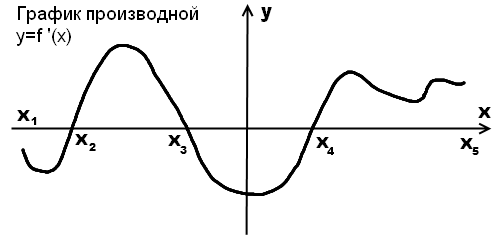
Функция y=f(x) возрастает на промежутках (x2;x3) и (x4;x5).

Функция y=f(x) убывает на промежутках (x1;x2) и (x3;x4).

Критические точки: x2, x3, x4.

Точка максимума — x=x3.

Точки минимума — x=x2 и x=x4.

С помощью графика производной y=f ‘(x)также можно сравнивать значения функции y=f(x). Такие задания рассмотрим позже.