Рассмотрим решение тригонометрических неравенств вида cosx>a на единичной окружности.
Косинус — это абсцисса точки. Значит, cosx=a в точках пересечения единичной окружности и прямой x=a (прямая, параллельная оси oy), cosx>a справа от этой прямой, cosx<a — слева. Поскольку мы рассматриваем решение неравенства cosx>a, нам нужна часть окружности, расположенная правее прямой y=a. Соответственно, от взаимного расположения окружности и этой прямой зависит решение неравенства cosx>a.
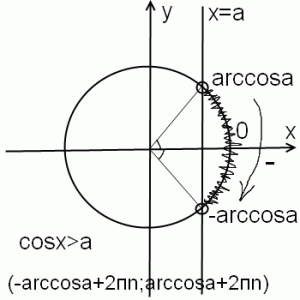
1) cosx>a при 0<a<1
На единичной окружности отмечает точки пересечения ее с прямой y=a. Первая точка — arccos a. Чтобы найти вторую, рассуждаем так: решения неравенства cosx>a лежат справа от этой прямой (заштриховываем соответствующую дугу окружности). Поэтому, чтобы попасть из 1й точки во вторую, идем по часовой стрелке. При таком обходе угол уменьшается. Доходим до нуля, дальше — отрицательные углы. Вторую точку отделяет от нуля такой же угол, что и первую. Но поскольку мы шли по часовой стрелке, ее берем со знаком минус.
Интервал записываем по возрастанию, поэтому сначала идет -arccos a, потом уже arccos a. С учетом периодичности синуса, к каждому из концов интервала прибавляем 2пn, где n — целое число (n принадлежит Z). Если неравенство нестрогое, точки закрашиваем и включаем в ответ (с квадратными скобками).
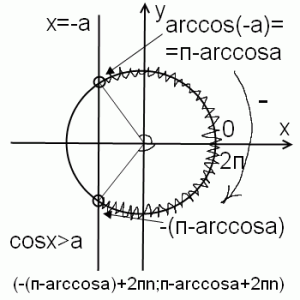
2) cosx>-a при 0<a<1
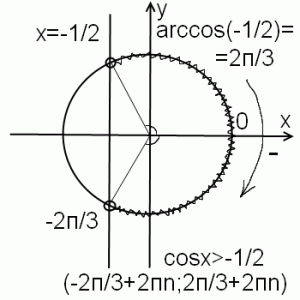
Рассуждения аналогичны предыдущему случаю. Отличие — нужно искать arccos(-a) (чуть позже я расскажу, как легко запомнить арккосинусы отрицательных чисел).
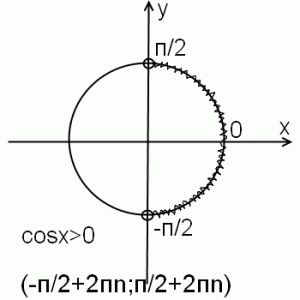
3) cosx>0
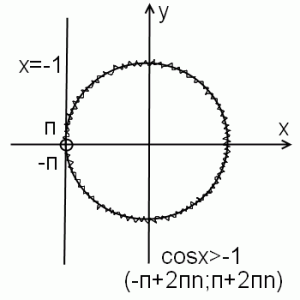
4) cosx>-1
За исключением одной точки,вся окружность лежит правее прямой y=a. Чтобы записать ответ в виде интервала, первой точкой берем -п. Поскольку во 2ю попадаем через полный оборот окружности, то есть через 2п, то -п +2п=п. К обоим концам интервала прибавляем 2пn.
![\[5)\cos x \geqslant - 1\]](https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-2db529c75db86b7466fc40eb30025549_l3.png "Rendered by QuickLaTeX.com")
В этом случае точки исключать не нужно, x — любое число: (-∞;+∞).
![\[6)\cos x \geqslant 1\]](https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-017c4def6cb5decc6a0e996bff5fd80c_l3.png "Rendered by QuickLaTeX.com")
Единственной точкой, удовлетворяющей данному условию, является 0. С учетом периодичности косинуса, решение — множество точек x=2пn.
7) cosx>a при a>1
Единичная окружность полностью лежит слева от прямой y=a, поэтому при таких a нет ни одной точки, удовлетворяющей условию cosx>a. Значит, решений нет.
8) cosx>-a при a>1
Единичная окружность целиком лежит правее прямой y=a, поэтому x — любое число: (-∞;+∞).
И в заключении — конкретный пример решения неравенства вида cosx>a:
