« »

Рубрика: Задание 7 ЕГЭ математика (производная и первообразная)

Угловой коэффициент касательной

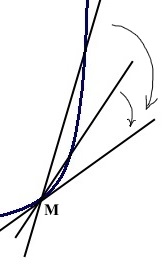
uglovoj-koehfficient-kasatelnoj

 

В школьной геометрии касательная к окружности определяется как прямая, которая имеет с окружностью только одну общую точку — точку касания.

 

В высшей математике касательная, проведённая в точке M — это предельное положение секущей MN.

 

 

 

 

 

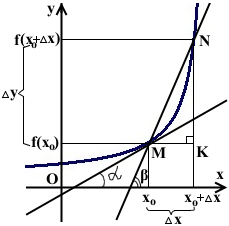
geometricheskij-smysl-proizvodnoj

Пусть дан график функции y=f(x).

Отменим на нём точку M, в которой существует касательная к графику, не параллельная оси абсцисс.

M(xо;f(xо)).

Зададим значению аргумента приращение Δx.

Значению аргумента xо+Δx на графике функции y=f(x) соответствует точка N(xо+Δx;f(xо+Δx)).

Угловой коэффициент секущей MN

равен

    \[ k_{MN} = tg\beta = \frac{{NK}}{{MK}} = \frac{{\Delta y}}{{\Delta x}} = \frac{{f(x_o + \Delta x) - f(x_o )}}{{\Delta x}} \]

Если приращение стремится к нулю (Δx→0), то секущая MN, поворачиваясь вокруг точки M, стремится к касательной, проведённой в точке M.

Если k — угловой коэффициент этой касательной, то

    \[ k \to \frac{{f(x_o + \Delta x) - f(x_o )}}{{\Delta x}}, \]

то есть

    \[ k = tg\alpha = \mathop {\lim }\limits_{\alpha \to \beta } tg\beta = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{f(x_o + \Delta x) - f(x_o )}}{{\Delta x}} = f^/ (x_o ) \]

Если касательная к графику функции в некоторой точке параллельна оси абсцисс, то угловой коэффициент такой касательной равен нулю.

 

Геометрический смысл производной:

Угловой коэффициент касательной к графику функции y=f(x), проведённой в точке с абсциссой xо, равен значению производной в точке касания:

k=f'(xо)

 

Так как угловой коэффициент прямой равен тангенсу угла α между прямой и положительным направлением оси абсцисс, то tgα=f'(xо).

 

Примеры.

№1

Найти угловой коэффициент касательной к графику функции

    \[ f(x) = \frac{1}{3}x^3 - 4x^2 - 5x + 1 \]

в точке с абсциссой xо=-2.
Решение:

    \[ f^/ (x) = \left( {\frac{1}{3}x^3 - 4x^2 - 5x + 1} \right)^/ = \frac{1}{3} \cdot 3x^2 - 4 \cdot 2x - 5 = x^2 - 8x - 5. \]

    \[ k = f^/ (x_o ) = f^/ ( - 2) = ( - 2)^2 - 8 \cdot ( - 2) - 5 = 15. \]

Ответ: 15.

№2

Найти абсциссу точки графика функции

    \[ f(x) = 11 - 3x - x^2 , \]

в которой угловой коэффициент касательной к графику равен -9.

Решение:

    \[ f^/ (x) = \left( {11 - 3x - x^2 } \right)^/ = - 3 - 2x. \]

    \[ k = f^/ (x_o ) = - 3 - 2x_o . \]

По условию, k=-9. Отсюда

    \[ - 3 - 2x_o = - 9 \]

    \[ x_o = 3. \]

Ответ: 3.

Ваш отзыв , 20 Июн 2021

Ваш отзыв