Рассмотрим задания из №6 ЕГЭ, в которых по графику функции требуется определить точки, в которых производная положительна либо отрицательна.
№1
На рисунке изображён график дифференцируемой функции y=f(x). На оси абсцисс отмечены восемь точек: x1, x2 ,x3, x4, … , x8. Среди этих точек найдите все точки, в которых производная функции f(x) положительна. В ответе укажите количество найденных точек.
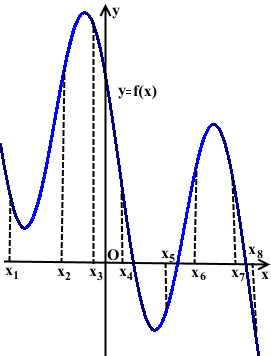
Решение:
Производная функции f'(x) положительна там, где функция y=f(x) :
f'(x)>0, если f(x) возрастает.
Выделяем промежутки возрастания функции y=f(x) и определяем количество точек, принадлежащих этим промежуткам.
Промежуткам возрастания функции y=f(x) принадлежат три точки: x2, x5 и x6.
Значит, производная функции в этих трёх точках положительна:
f'(x2)>0,
f'(x5)>0,
f'(x6)>0.
Ответ: 3.
№2
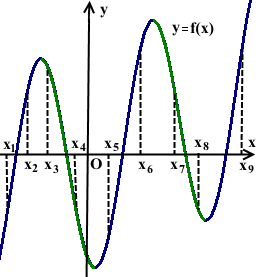На рисунке изображён график функции y=f(x) и отмечены девять точек на оси абсцисс: x1, x2 ,x3, x4 …x8, x9. В скольких из этих точек производная функции f(x) отрицательна?
Решение:
Производная функции f'(x) отрицательна там, где функция y=f(x) убывает:
f'(x)<0, если f(x) убывает.
Выделяем промежутки убывания функции y=f(x) и определяем количество точек, принадлежащих этим промежуткам.
Промежуткам убывания функции y=f(x) принадлежат четыре точки: x3, x4, x7 и x8. Значит, производная в этих четырёх точках отрицательна:
f'(x3)<0, f'(x4)<0, f'(x7)<0, f'(x8)<0.
Ответ: 4.
№3
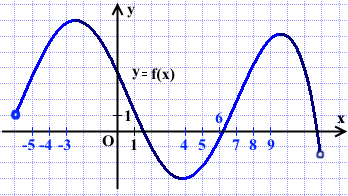На рисунке изображен график функции y=f(x), определенной на интервале (−6; 12). Определите количество целых точек, в которых производная функции положительна.
Решение:
Производная функции f'(x) положительна там, где функция y=f(x) возрастает.
Выделяем промежутки возрастания.
Целые точки, входящие в промежутки возрастания: -5; -4; -3; 4; 5; 6; 7; 8; 9.
Всего девять точек.
Ответ: 9.