Рассмотрим задания из №7 ЕГЭ, в которых по данному графику производной функции нужно найти точки минимума функции.
№1
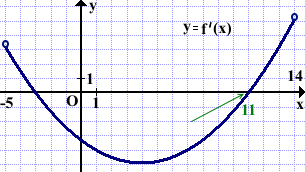
На рисунке изображён график функции y=f'(x) — производной функции f(x), определённой на интервале (-5;14). Найти точку минимума функции f(x).
 Решение:
Решение:
В точке минимума производная непрерывной функции обращается в нуль и при переходе через точку минимума производная меняет свой знак с минуса на плюс.
Таким образом, график производной в точке минимума пересекает ось абсцисс снизу вверх.
Значит, точка x=11 — точка минимума функции f(x).
Ответ: 11.
№2
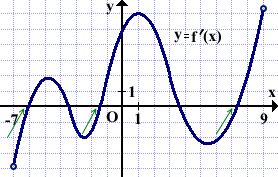
На рисунке изображён график функции y=f'(x) — производной функции f(x), определённой на интервале (-7;9). Найти количество точек минимума функции f(x).
 Решение:
Решение:
При переходе через точку минимума график производной пересекает ось абсцисс снизу вверх.
График производной пересекает ось Ox снизу вверх три раза. Значит, функция имеет три точки минимума.
Ответ: 3.
№3
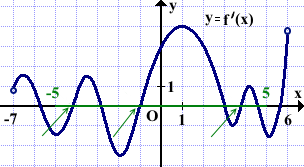
На рисунке изображён график y=f'(x) — производной функции f(x), определённой на интервале (-7;6). Найти количество точек минимума функции f(x), принадлежащих отрезку [-5;5].
 Решение:
Решение:
Выделяем отрезок [-5;5].
При переходе через точку минимума график производной пересекает ось абсцисс снизу вверх.
На данном отрезке график производной пересекает ось Ox снизу вверх трижды. Значит, функция f(x) имеет на этом отрезке три точки минимума.
Ответ: 3.