В №7 ЕГЭ несколько видов заданий, в который нужно по графику функции найти точки, в которых производная обращается в нуль.
Как найти, в каких точках производная равна нулю на графике функции?
В точках, в которых производная равна нулю, касательная к графику функции параллельна оси абсцисс.
Это могут быть точки экстремума (те из них, в которых производная существует):

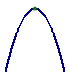
Либо точки перегиба:
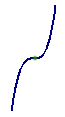
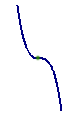
В окрестности точки экстремума график лежит по одну сторону от касательной, в окрестности точки перегиба — по разные стороны.
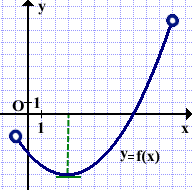 1)На рисунке изображён график функции y=f(x), определённой на интервале (−1; 11). Найдите корень уравнения f'(x)=0.
1)На рисунке изображён график функции y=f(x), определённой на интервале (−1; 11). Найдите корень уравнения f'(x)=0.
Решение:
Касательная к графику функции y=f(x) параллельна оси абсцисс в точке x=3.
Следовательно, корнем уравнения f'(x)=0 является x=3.
Ответ: 3.
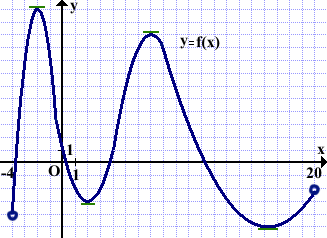 2)На рисунке изображён график функции y=f(x), определённой на интервале (−4; 20). Найти количество решений уравнения f'(x)=0.
2)На рисунке изображён график функции y=f(x), определённой на интервале (−4; 20). Найти количество решений уравнения f'(x)=0.
Решение:
Касательная к графику параллельна оси абсцисс в четырёх точках.
Значит, уравнение f'(x)=0 имеет четыре решения.
Ответ: 4.
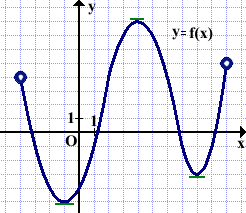 3)На рисунке изображен график функции y=f(x), определенной на интервале (−4; 10) . Найдите количество точек, в которых производная функции f(x) равна 0.
3)На рисунке изображен график функции y=f(x), определенной на интервале (−4; 10) . Найдите количество точек, в которых производная функции f(x) равна 0.
Решение:
Касательная к графику параллельна оси Ox в трёх точках.
Таким образом, производная функции f(x) равна 0 в трёх точках.
Ответ: 3.
В этих примерах мы рассматривали график функции y=f(x)!
Задания, в которых надо определить в каких точках производная равна нулю на графике производной y=f'(x), решаются иначе!