Эта ассоциация позволяет легко запомнить формулу для решения частного случая тригонометрического уравнения cosx=1.
Как и другие частные случаи косинуса, решение уравнения cosx=1 удобнее всего рассматривать на единичной окружности.
Ассоциация прежняя: косинус-колобок. И начинаются они одинаково, на ко-, и округлые буквы в его названии: c, o, s.
А колобку с его фигурой удобно двигаться вправо-влево, но никак не вверх-вниз. Влево-вправо у нас движение по оси ox, а значит, косинус — это x.
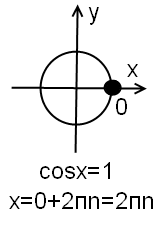
Нам нужны точки, в которых x равен 1, поэтому идем вправо. Попадаем в 0. Это только одна из точек, в которой cosx=1.
Через полный оборот окружности мы снова попадем в точку, в которой косинус равен единице.
Если идти против часовой стрелки, этой следующей точкой будет 2π, по часовой стрелке — -2π. Через 2,3,4 и т.д. оборота мы снова попадаем в точки, в которых cosx=1.
Чтобы учесть все такие точки, 2π умножаем на n, где n — целое число. Таким образом, окончательно имеем: если cosx=1, то x=0+2πn, или просто x=2πn.
решение уравнения cosx=1